Introduction:
In the annals of history, certain figures shine brightly, illuminating the path for future generations with their intellect and innovation. Among these luminaries stands Brahmagupta, a mathematical genius and astronomer whose contributions to the fields of mathematics and astronomy continue to reverberate through time. Join me on a journey through the life and expertise of this remarkable scholar.
Early Life:

Brahmagupta was born in 598 CE in the city of Bhinmal, located in the northwest region of ancient India, now part of Rajasthan. While details about his early life are scarce, it is believed that he received his education in astronomy and mathematics in the ancient Indian city of Ujjain, a renowned center of learning during that era.
Expertise in Mathematics:
Brahmagupta’s expertise in mathematics was truly revolutionary, shaping the course of mathematical thought for centuries to come. His most famous work, the “Brahmasphutasiddhanta” (The Correctly Established Doctrine of Brahma), written in 628 CE, is a foundational text in the history of mathematics.
Brahmagupta’s theorem
It is also known as Brahmagupta’s formula, is a fundamental result in geometry discovered by the Indian mathematician Brahmagupta, who lived during the 7th century CE.
This theorem provides a method for finding the area of a cyclic quadrilateral, which is a quadrilateral with all its vertices lying on the circumference of a circle.
Statement of the Theorem:
Brahmagupta’s theorem states that the area (A) of a cyclic quadrilateral with side lengths a, b, c, and d can be calculate using the following formula:
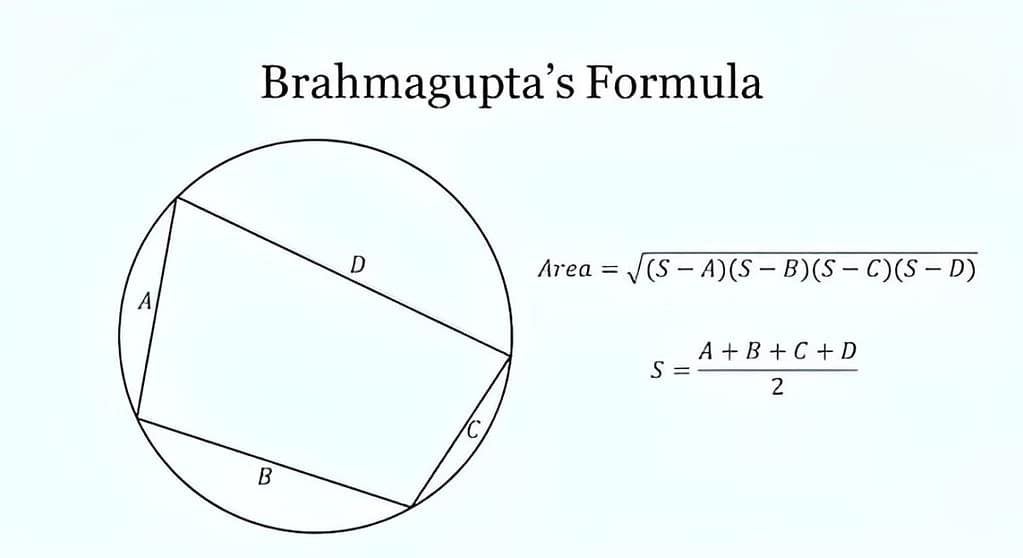
where s is the semiperimeter of the quadrilateral.
Understanding the Theorem:
Firstly, we understand Brahmagupta’s theorem, it’s helpful to visualize a cyclic quadrilateral inscribed within a circle. Each side of the quadrilateral corresponds to a chord of the circle, and the area of the quadrilateral is determined by the lengths of these chords and the distance from the center of the circle to each chord.
Brahmagupta’s theorem essentially expresses the area of the cyclic quadrilateral in terms of the lengths of its sides, without directly involving the angles of the quadrilateral.
This feature renders it a particularly useful tool for calculating the area of such shapes, especially in cases where the angles are unknown or challenging to ascertain.
Applications:

Brahmagupta’s theorem finds applications in various areas of mathematics, particularly in geometry and trigonometry. It provides a simple and elegant method for calculating the area of cyclic quadrilaterals, which arise frequently in geometric problems involving circles.
Furthermore, Brahmagupta’s theorem serves as a precursor to more advanced concepts in geometry, such as the Brahmagupta-Fibonacci identity, which relates the area of a cyclic quadrilateral to the product of the radii of four circles that are tangent to each side of the quadrilateral.
Zero as a Number:

One of Brahmagupta’s most significant contributions to mathematics was his development of the concept of zero as a number. Before Brahmagupta, people used zero as a mere placeholder in numerical systems, not recognizing it as a standalone number. Brahmagupta’s recognition of zero as a number with its own properties paved the way for the development of the decimal system and laid the groundwork for modern mathematics.
Algebraic Contributions:
In addition to his work on zero, Brahmagupta made significant contributions to algebra. He solved quadratic equations with both positive and negative roots and developed methods for solving simultaneous linear equations. His mathematical insights were not only profound but also practical, demonstrating a deep understanding of real-world applications.
Expertise in Astronomy:

Brahmagupta was also a renowned astronomer who made significant contributions to the field of astronomy. He wrote extensively on topics such as planetary motion, eclipses, and celestial phenomena, providing detailed observations and mathematical explanations for these phenomena.
“Brahmasphutasiddhanta”:

One of Brahmagupta’s most famous astronomical works is the “Brahmasphutasiddhanta,” which contains detailed descriptions of planetary motion, the positions of the stars, and the calculation of eclipses. His observations of celestial bodies and their movements helped to advance the field of astronomy in ancient India and laid the groundwork for future astronomical research.
Legacy:
Brahmagupta’s legacy is profound and far-reaching, with his contributions to mathematics and astronomy continuing to influence scholars and scientists to this day.
His recognition of zero as a number and his insights into algebra laid the foundation for modern mathematics, while his work in astronomy provided valuable observations and explanations of celestial phenomena.
Conclusion:
In conclusion, we reflect on Brahmagupta’s early life and expertise. In contemplating Brahmagupta’s theorem, we are reminded of how knowledge endures and intellectual curiosity transforms. His brilliance continues to inspire generations of scholars and serves as a testament to the potential of human intellect to shape the course of history. Through his pioneering work in mathematics and astronomy, Brahmagupta left an indelible mark on the world, reminding us that the pursuit of knowledge knows no bounds.


